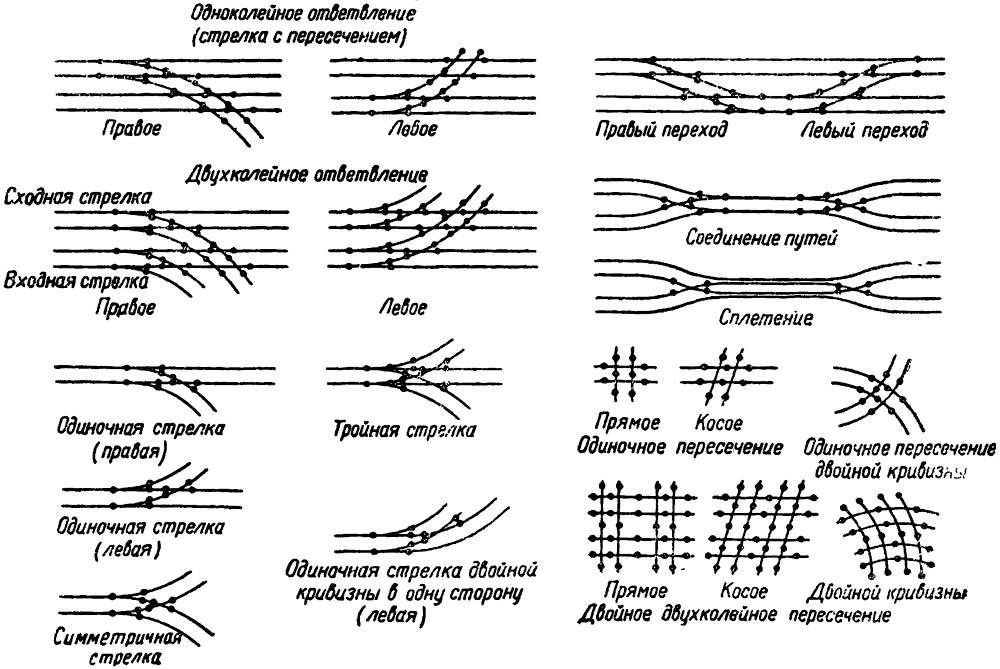
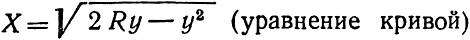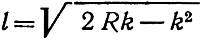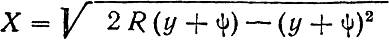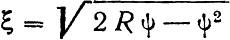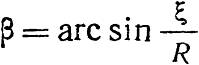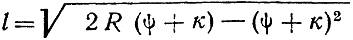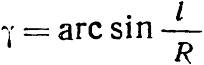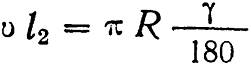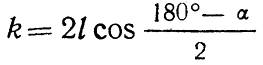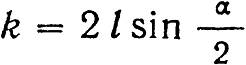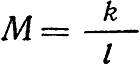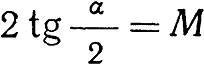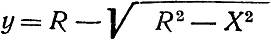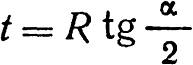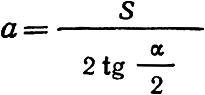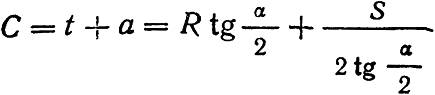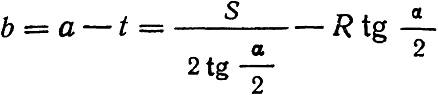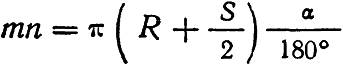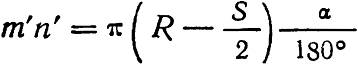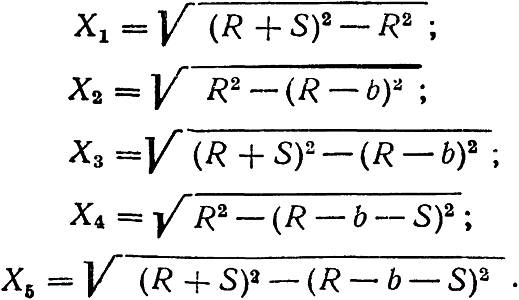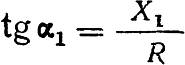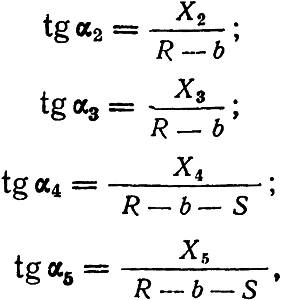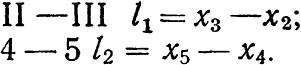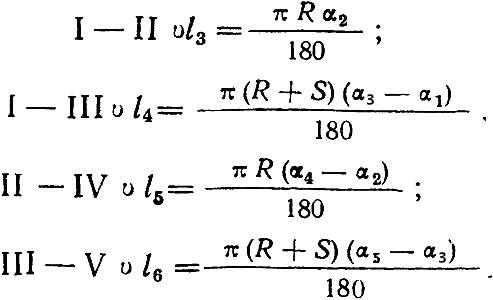Узлы трамвайных путей составляются из отдельных стрелочных переводов и пересечений, поэтому расчет узлов сводится к расчету отдельных стрелочных переводов. Типы стрелочных переводов и пересечений показаны на рис. 1.
Габаритные размеры стрелочных переводов и крестовин пересечения трамвайного пути определяются по невыгодному совпадению размеров ходовых частей вагона и колеи.
Рис. 1. Типы стрелочных переводов и пересечений трамвайного пути.
Расчет стрелок трамвайного пути
Расчет стрелочного перевода трамвайных путей заключается в определении геометрических размеров его элементов, т. е. стрелки, крестовины и переводной кривой.
Стрелка может рассчитываться по двум способам: без пересечения рамного рельса или с пересечением его. В первом случае кривая рабочего канта стрелки является касательной к рабочему канту рамного рельса, во втором случае кривая рабочего канта стрелки пересекает рабочий кант рамного рельса и является касательной к линии, параллельной ему, находящейся на расстоянии ψ от рабочего канта рамного трамвайного рельса.
Стрелка без пересечения рамного рельса трамвайного пути
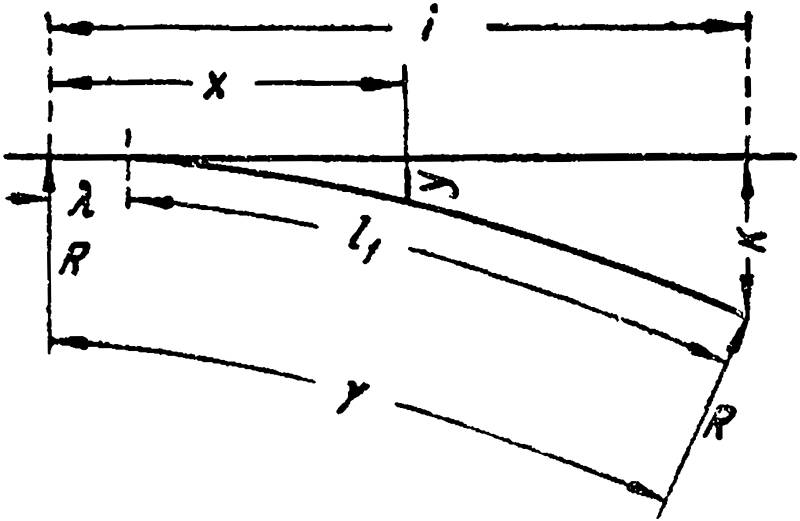
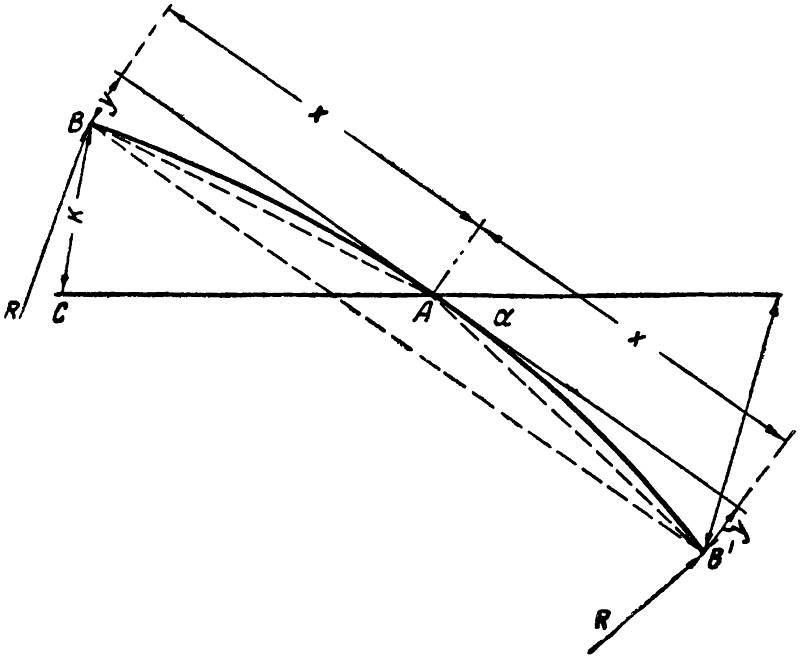
Расстояние от начала пера до тангенса в стрелке (рис. 2) равно:
– уравнение кривой,
где: R – радиус наружной нитки стрелки;
y – ордината кривой пера у начала остряка (обычно y = 8 мм).
Рис. 2. Эпюра стрелки без пересечения рамного рельса трамвайного пути.
Длина стрелки от математического острия (точки касания) пера до стыка у пяты стрелки:
где k – расстояние между рабочими кантами прямого и кривого рельсов в стыке у пяты стрелки (раствор стрелки).
Величина k зависит от конструкции стрелки и радиуса кривой, но для удобства устройства стыков не может приниматься меньше 200 мм.
Действительная длина стрелки от стыка, у начала стрелки, до стыка, у пяты стрелки, отличается от теоретической длины на величину λ, которая показывает расстояние от математического острия (от тангенса) до стыка у начала стрелки.
Минимальное расстояние от начала пера до начала рамного рельса (остряка) трамвайных путей должно приниматься с учетом обеспечения возможности соединения стрелки с рельсом нормальной шестидырной накладкой. Обычно это расстояние принимается равным 600 мм. При этом условии расстояние от тангенса до стыка составит:
– при радиусе стрелки 20 м: λ = 0 мм;
– при радиусе стрелки 30 м: λ = 100 мм;
– при радиусе стрелки 50 м: λ = 300 мм;
И действительная длина стрелки l1 = l – λ.
Центральный угол γ, соответствующий длине кривой при абсциссе l равен γ = arc sin (l/R); длина теоретической кривой – vl2 = πR(γ/180°).
Действительная длина кривой до стыка – vl3 = vl2 – λ.
Стрелка с пересечением рамного рельса трамвайного пути
В этом случае уравнение кривой (рис. 3) принимает следующий вид:
где ψ – расстояние между касательной и рабочим кантом рамного рельса.
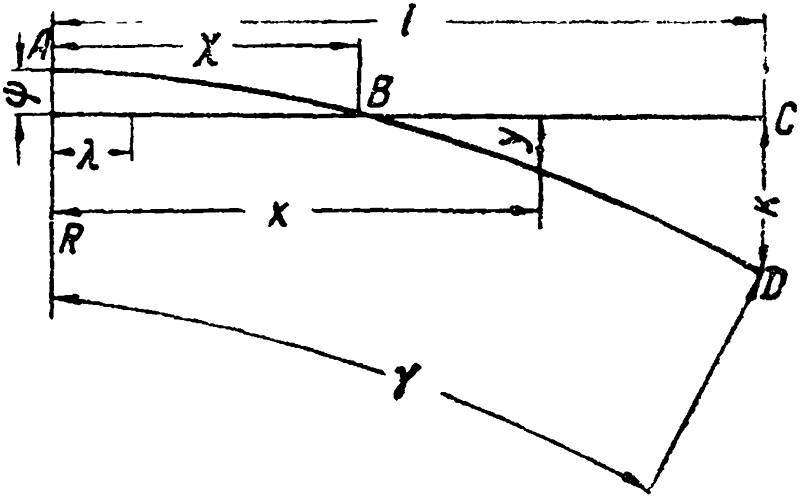
Рис. 3. Эпюра стрелки с пересечением рамного рельса трамвайного пути.
Расстояние от точки В пересечения кривой остряка с рабочим кантом рамного рельса трамвайных путей до тангенса равно:
Угол удара в точке В составит:
Длина стрелки от математического острия (точки касания) до стыка в пяте стрелки:
Величина k определяется, так же, как и для стрелки, без пересечения рамного трамвайного рельса.
Действительная длина стрелки равна: l1 = l – λ.
Центральный угол γ, соответствующий длине кривой при абсциссе l, равен:
Длина теоретической кривой (от А до D) составит:
B действительная длина кривой до стыка: vl3 = vl3 – λ.
Расчет крестовин трамвайных путей
При расчете крестовин трамвайного пути определяются:
– угол крестовины, образуемый рабочим кантом прямого рельса или касательной к рабочему канту кривого рельса в точке пересечения рабочих кантов рельсов (математический центр крестовин);
– радиус кривизны крестовины;
– длина хвостов по прямому и кривому направлениям, принимаемая по конструктивным соображениям;
– растворы крестовин – расстояние между рабочими кантами в концах крестовины.
Прямая крестовина трамвайного пути
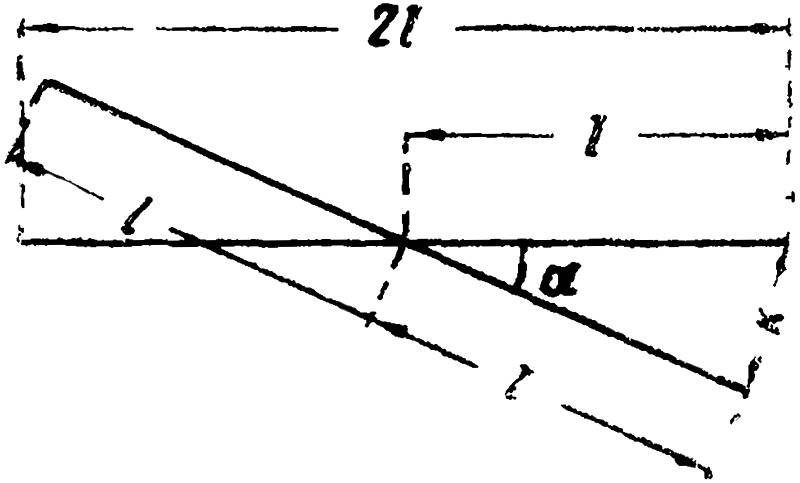
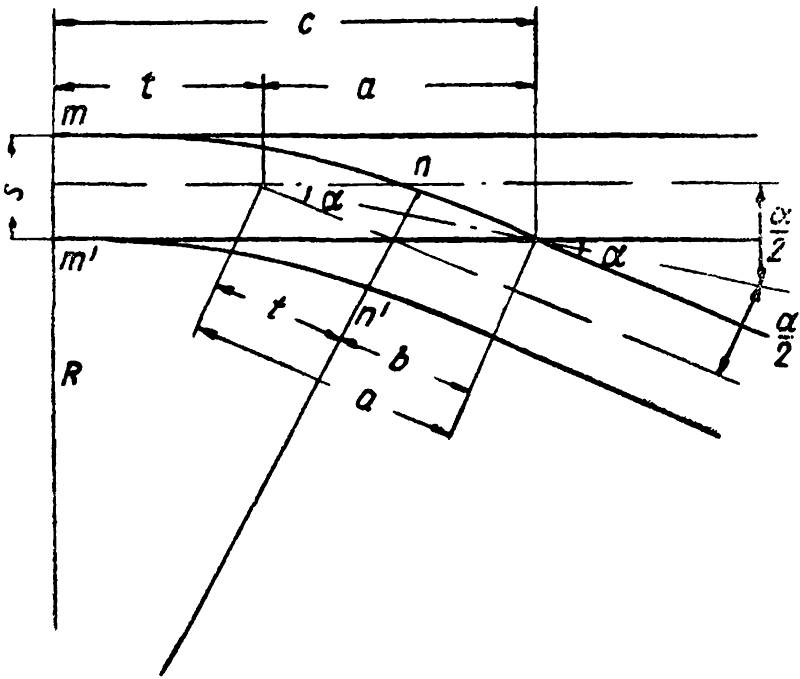
Угол прямой крестовины α (рис. 4) образуется пересечением рабочих кантов рельсов в математическом центре крестовины.
Рис. 4. Эпюра прямой крестовины трамвайного пути.
Раствор прямой крестовины выражается формулой:
или
где: l – длина хвостов;
α – угол крестовины.
Марка прямой крестовины определяется отношением раствора к длине хвостов:
Наиболее часто встречающиеся марки трамвайных крестовин: М = 1:4 и Μ = 1:6.
Угол крестовины для этих марок может быть определен по формуле:
Кривая крестовина трамвайного пути
Угол кривой крестовины односторонней кривизны (рис. 5) образуется пересечением рабочего канта прямого трамвайного рельса с касательной рабочего канта кривого рельса в математическом центре крестовины.
Рис. 5. Эпюра кривой крестовины трамвайного пути.
Координаты кривой исчисляются по формуле:
Растворы крестовины k и k1 определяются при известных величинах – угле крестовины α, длине хвостов (АВ, АС, АВ’ и АС’) из рассмотрения и решения треугольников, образуемых хордой, стягивающей дугу ВВ’ и хордой, стягивающей дугу АВ и АВ’.
По этому же принципу рассчитываются и крестовины двойной кривизны.
Расчет стрелочного перевода трамвайных путей с прямой крестовиной
Если радиус стрелки по оси пути равен R, угол прямой крестовины α, то, обозначая ширину колеи через S имеем (рис. 6) тангенс:
Рис. 6. Эпюра стрелочного перевода трамвайного пути с прямой крестовиной.
Расстояние от угла поворота до математического центра крестовины по оси равно:
Полная длина перевода от начала кривой до математического центра крестовины составит:
Прямая вставка – расстояние между концом кривой и математическим центром крестовины – равно:
Длина кривой по наружной нитке:
Длина кривой по внутренней нитке:
Расчет стрелочного перевода трамвайных путей с кривой крестовиной и пересечением второго пути
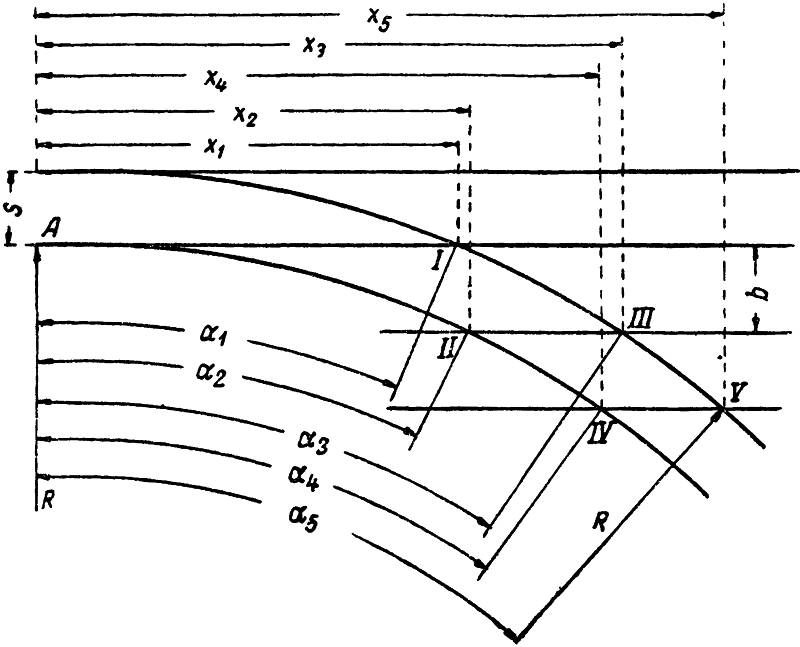
При радиусе пересечения крестовины, равном радиусу стрелки, координаты математических центров крестовин (рис. 7) получатся при радиусе по внутренней нитке R и ширине колеи S и ширине междупутья b следующими:
Рис. 7. Эпюра стрелочного перевода трамвайного пути с кривой крестовиной и пересечением.
Углы α1–α5, определяющие углы крестовин, исчисляются на основе следующих уравнений:
Длина прямых составляет:
Длина кривых составляет:
Новостройки симферополь квартиры в новострои ках симферополя.