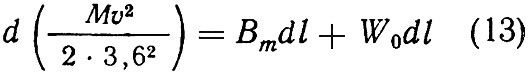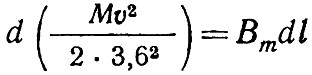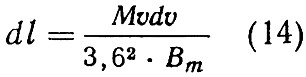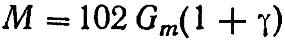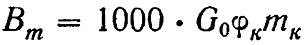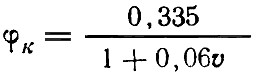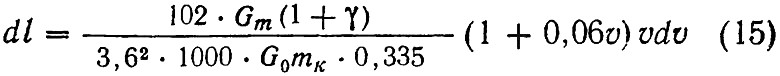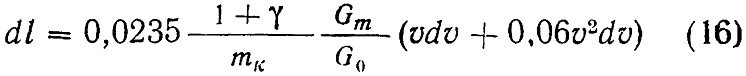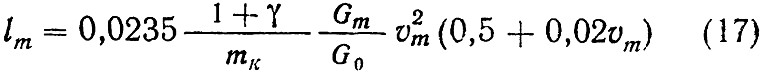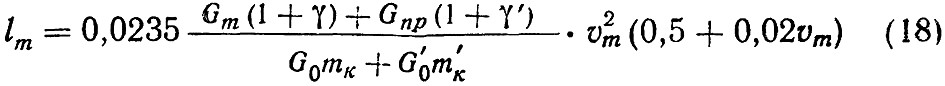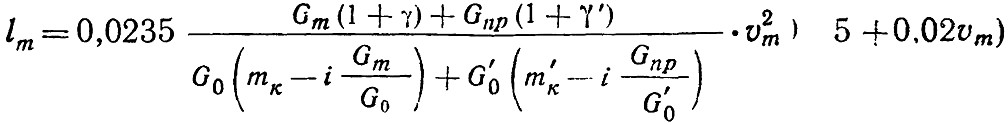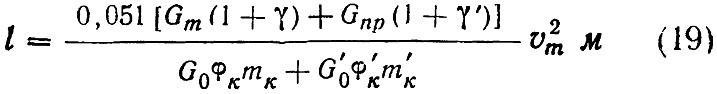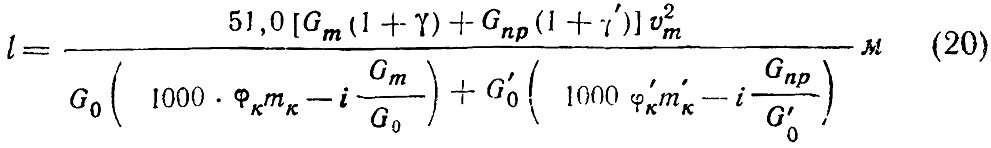Тормозные параметры вагонов подвижного состава трамвая — Часть 3 из 3: Уравнение кинетической энергии поезда, масса вагона, тормозная сила и тормозной путь

Уравнение кинетической энергии поезда, состоящего из одного моторного трамвайного вагона, может быть представлено в следующем виде:

где: M — приведенная масса поезда в кг·сек²/м;

v — скорость при торможении в км/час.

Левая часть уравнения (13) представляет собой дифференциал приращения кинетической энергии трамвайного вагона при торможении на пути l.

Правая часть уравнения (13) показывает работу тормозной силы на этом же пути.

Ввиду того, что член W₀Dl мал по сравнению с B_mDl, уравнение (13) можно представить в следующем виде:

или

Масса вагона выражается так:

где: G_m — вес моторного вагона с пассажирами в т;

1+γ — коэффициент инерции вращающихся частей.

Тормозную силу можно выразить:

Принимая коэффициент φ_к для колесно-колодочного тормоза по формуле Московского энергетического института, имеем:

Подставим значения M, B_m и φ_к в формулу (14), получим:

или

Далее проинтегрируем левую часть уравнения по l в пределах от нуля до l_m, а правую — по v в пределах от v = v_m до v = 0. В результате получим:

где: l_m — длина тормозного пути в м;

v_m — скорость начала торможения.

Если поезд будет состоять из моторного и прицепного вагонов, а φ_к примем примерно одинаковым для обоих вагонов, уравнение (17) примет вид:

где: G_пр — вес прицепного вагона с пассажирами;

G₀‘ — вес прицепного вагона без пассажиров;

1 + γ’ — коэффициент инерции вращающихся частей прицепного вагона;

m_к‘ — коэффициент нажатия тормоза прицепного вагона.

При движении поезда на спуске тормозной путь будет равен:

Величину тормозного пути двухвагонного поезда на площадке можно также определить по формуле:

Тормозной путь двухвагонного поезда на спуске составляет:

Где: i — величина спуска в кг/т;

φ’_к — коэффициент трения между колодкой и тормозным элементом на прицепном трамвайном вагоне.

Ориентировочные значения коэффициента инерции вращающихся частей подвижного состава (1+γ) могут быть взяты из табл. 62.

Все части: 1 | 2 | 3